A mathematical approach to Zoom wait times

As a large fraction of the world is working remotely, a lot of people's days are spent jumping between video conference calls. One question that might occur when someone joins a video conference call is how much time you should wait for the other person to join. We're going to use a simplistic mathematical model for the waiting time on a 1:1 video conference call using a famous probability distribution.

Unlocking efficient with a mathematical approach for waiting on a Zoom call

The problem of modeling waiting times is not new, it has been widely studied in the past particularly in areas like transportation, where it has been observed that waiting times in train and bus networks tend to follow an exponential distribution. We are going to assume that the problem of someone joining a video call is similar, from a probabilistic standpoint, to that of a train arriving at a railway station.

The exponential distribution is a continuous distribution defined by the following probability density function in which t is, in this case, the waiting time before the other person joins the call and \(\mu\) is the mean of the distribution

\(f(t) = \frac{e^{-t/\mu}}{\mu} \text{ , $t \ge 0$} \)

We can calculate the probability that someone takes more than \(T\) minutes to join a call by integrating \(f\)

\(P(t>T)= 1 - \int_{0}^{T}f(t) = e^{-T/\mu}\)

Crunching the numbers: determining how long to wait on a Zoom call before leaving

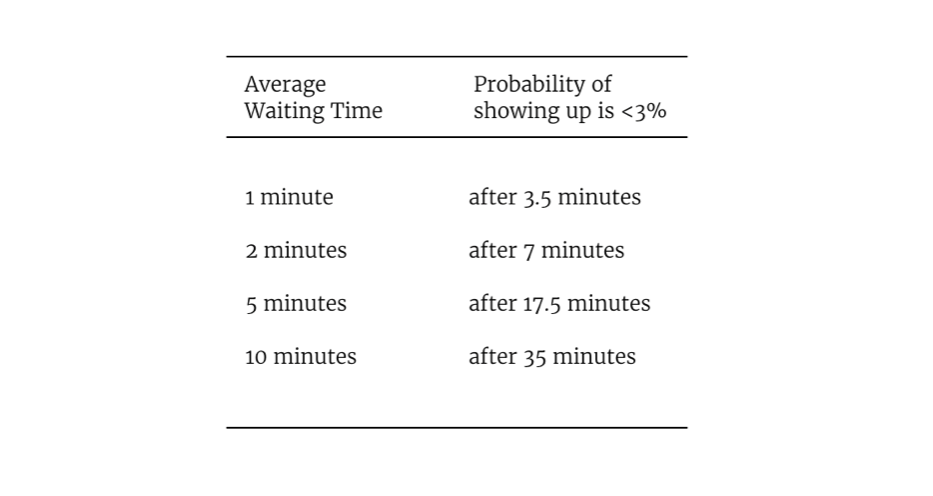
Now, the only thing we need to do is estimate the mean of the distribution. For that we’re going to use a sample of past calls and calculate the mean waiting time for those calls. In our case, we are also going to separate our calls in 2 types: Hiring Interviews and Sales Meetings. The average waiting time for our sample is 1.5 min for Hiring Interviews and 3 min for Sales Meetings. Based on these values we can now plot the waiting time probabilities for the 2 cases.

We can see that, for Hiring Interviews, the probability of waiting more than 5 minutes is relatively low - approximately 3% - whereas to get to the same probability on Sales Meetings we need to wait around 10 minutes.

This is a simplistic model but having an idea of how much time you should wait on a video call before you can confidently say that someone is unlikely to show up can have a considerable impact on the time and productivity losses across teams and companies.

 Amplemarket helps you find and get in touch with your next customers in the most efficient and personalized way possible.